L’élasticité : le graal du Revenue Management. Insaisissable. Pourtant, on nous la vend comme une formule toute simple qui revient à : e = dQ/dP. C’est beau, c’est simple, mais c’est faux.
On retrouve cette formule ou des formulations similaires partout, sur Wikipédia comme sur les sites internet parlant d’économie ou de RM. Alors une fois pour toute, pourquoi c’est faux ?
Elasticité, l’exemple de l’hôtellerie
Prenons un hôtel de 400 chambres. Un remplissage prévu de 200, avec un prix à 100€. Un CA prévu de 20 000€ donc (100€ x 200).
Si l’on suppose que l’élasticité est connue, qu’elle vaut disons -1,5 (ce qui veut dire que si l’on baisse le prix de 10%, nous aurions 15% de demande en plus), quelles en sont les conséquences ? Faisons des tests :
- Prix -10% / Volume +15%. CA = 20 700€ (90€ x 230)
- Prix -15% / Volume +22,5%. CA = 20 825€ (85€ x 245)
- Prix -20% / Volume +30%. CA = 20 800€ (80€ x 260)
Le CA augmente d’abord en fonction de la baisse de prix, puis redescend. Pourquoi ? Rappelez-vous les mathématiques du lycée : c’est parce que le CA décrit une parabole négative (comme la trajectoire d’un caillou quand on le lance devant soi).
Mathématiquement, c’est une fonction du 2nd degré que l’on peut écrire CA(x) = P * V (1+x) * (1+ex), où x est la variation de prix, P et V les prix et volume initiaux, e l’élasticité. Une fonction en ex², avec e négatif.
Si l’élasticité est inférieure à -1, ce que tout le monde convient (sauf exception), cette fonction atteint son maximum en un point unique, comme le caillou qu’on lance et qui atteint son apogée quelque part. Ce point unique s’obtient quand la dérivée de la fonction est nulle. C’est le cas lorsque x prend la valeur -(e+1)/2e (la dérivée est nulle quand 2ex + e+1 = 0. Dans notre exemple avec une élasticité à -1,5 la valeur de x qui maximise la CA vaut -0,5/6 = -17%).
Il faudrait donc faire une remise de 17% pour maximiser le CA. C’est l’optimum. Après on rentre chez soi car toute autre action détruirait de la valeur. On ne fera pas mieux.
Allons plus loin, ce calcul nous donne l’équation complète produisant la « valeur optimale » de remise qui maximiserait le CA pour chaque valeur d’élasticité (dès lors que le volume généré reste dans les limites de capacité). Nous pourrions alors établir une courbe de valeurs optimales : c’est la fonction f(e) = -(e+1)/2e qui varie en fonction de l’élasticité e.
De façon bien curieuse, cette courbe tend vers -50% quand l’élasticité tend vers l’infini (dans les négatifs). Ce qui voudrait dire, autre absurdité, que quelque soit le point de départ, aucune situation ne peut conduire à améliorer son chiffre d’affaires pour une remise de plus de 50%.
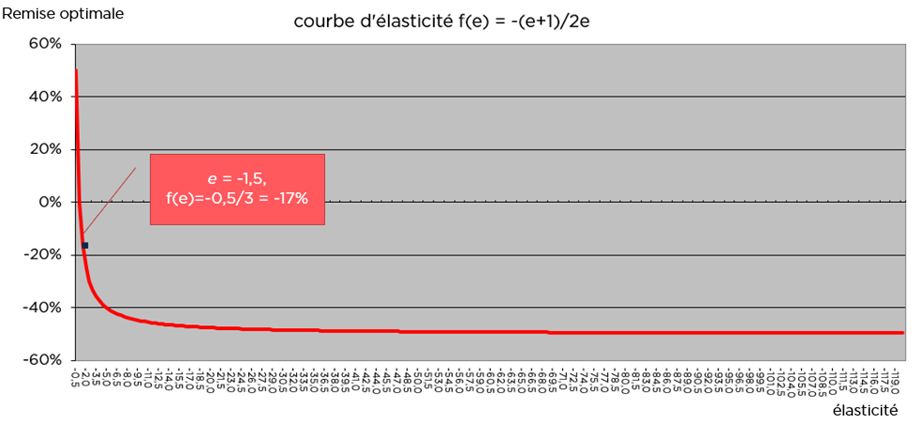
Courbe de l’élasticité
Mais pourquoi est-ce faux ?
C’est ce que nous dit la fonction d’élasticité si l’on considère qu’elle vaut e=dQ/dP. Car on n’a pris aucune hypothèse supplémentaire. Nous avons uniquement écrit l’équation qui en découle, et dérouler le raisonnement jusqu’au bout.
On sent bien que c’est faux et qu’il n’existe pas de « remise optimale », de « prix optimal » qui viendrait une fois pour toute maximiser le CA.
C’est faux car l’élasticité est bien plus complexe.
Elle est différente en fonction du prix initial, du lead time, du marché, du canal de vente, de la typologie de client, du produit acheté. Le niveau de granularité est l’un des problèmes. Il faudrait aller au croisement de toutes ces dimensions, mais alors on a trop peu de points d’observations. Et puis le calcul doit rester juste au voisinage du point de départ pour être juste, sur de toutes petites variations. Or, dans les métiers de l’hébergement, nous ne sommes pas à la pompe à essence. Les prix varient sur des amplitudes importantes. On se voit mal faire une baisse de prix de 0,04%.
De plus, la réponse de la demande a une baisse de prix n’est pas la même en fonction d’habillage du prix (en valeur, en prix barré, en remise en %, en nuits gratuites…) et en fonction de sa communication (mise en avant, budget marketing pour de la pub, …).
Et puis il y a des effets exogènes : réponse des concurrents, effets de cannibalisation sur des produits de substitution…
Pour aller plus loin et en finir avec l’élasticité, nous vous invitons à lire notre précédent article sur le sujet.
Bref, réduire l’élasticité à une équation simpliste et essayer d’en tirer profit est absurde. A de rares exceptions près, elle est non seulement impossible à mesurer mais aussi très difficile à manipuler.
Le RM a mille choses de plus intelligent à faire. Et essayer d’atteindre ce graal, qui est davantage fait pour amuser la galerie que pour piloter son Yield efficacement, n’en est pas une.
Mots-clés : Élasticité, Revenue Management, volume, valeur optimale, chiffre d’affaires

